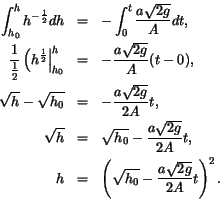Leaky-Bucket Experiment
Haefner/Powell
BIOL/MATH 4230 -
BioMath and Modeling
February 4, 2002
Lab Dates: February 4 and 11 Rough Draft (Group) due Febuary 15

A draining ``bucket'' during the February 5 lab.
This exercise has two parts: a model formulation and
calibration phase and a model validation or test phase. In
the first, students create a model in addition
to that based on Torricelli's Law and
choose the placement and shape and sizes of holes in buckets
to parameterize their models. In the second, an ``Evil Genius''
creates buckets with holes for students to test their models
against.
The following materials are needed.
- 1-2 quart plastic jugs such as those containing milk or
juice for use as the leaky buckets
- Drill and bits to create circular holes
- Scapels for cutting non-circular holes and removing burrs
- Stop watches
- Graduated cylinders for volume measurements
- Plastic dish washing tubs for water if a large sink is
not available
- Ring stands and plates for elevating the buckets
It is up to the students to ensure that they have plans to
measure all the parameters needed in their models. This may
involve different levels of ingenuity, flexibility, and
special equipment from the instructors, depending on the
models used.

A creating a ``bucket'' during the February 5 lab.
The Evil Genius will play by a few rules to ensure that
unreasonable test buckets are not created. For example, if E.G. wishes to
cut more than one hole, he should cut the holes at the same vertical level.
In particular, similar plastic jugs will be used. Holes on more than one
level will not be used. Otherwise, shape, size, and number of holes will
be freely created.
This exercise can be tuned for more or less difficulty depending on
instructors' aims and students' abilities. For example:
- Use a bucket with a regular, but vertically-varying cross-section.
- Put holes at different levels to illustrate problems with coupled
models.
- Vary the fluid or change the surface tension by adding a drop or two
of dish-washing liquid.
- Alter the local gravity field, or induce a time-varying gravity field
(just joking).

Students collecting data during the February 5 lab.
The general purpose of this lab exercise is to
- Introduce the concepts of a mathematical model of a
physical system,
- Instill in you the value of multiple working hypotheses
and alternative models,
- Force you to confront the messy attributes of real world
data as they relate to quantitative predictions, and
- Give you more practice in technical, scientific report writing.
The following specific objectives of the leaky bucket
model will
determine what kinds of models you build and how you go about
testing them.
- The question of interest is: ``Will the poor students
correctly predict the time required for the bucket
to empty, and thereby save their lives?''
- To solve the problem, the students will create 2 models
(or more, but 2 is plenty) which will allow the students
to determine the emptying time. The models must be
``signficantly different'' from each other.
- The students will have the opportunity to calibrate
their models (i.e., estimate parameters) on data they collect.
- The models, however, must be applicable to different
containers which were not available when the models were created
and calibrated. These new containers will differ from the first
by having holes of (slightly) different sizes, number, and shapes. The
container shapes will be similar. In other words, the models
must have a minimal degree of ``generality'' in the sense that
they will work on these new containers.
The tasks to complete are:
- Define the models
- Define the experimental protocol needed to estimate
the parameters
- Do the measurements and estimate the parameters
- Verify that the model does ``acceptably well'' (to be
defined by the modelers) on the original containers
- Apply the models to the new containers supplied by the
Evil Genius
- Answer the questions: ``Did we survive the guillotine?''
and ``Which model did best? Why?''
![\includegraphics[width=6.5in]{bucket.ps}](img2.gif)
The Torricelli model for the draining bucket is based on two physical
concepts:
- The Bernoulli relationship between pressure,
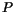 , density,
, density, 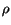 and speed,
and speed, 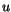 for fluid along a streamline:
for fluid along a streamline:
- The hydrostatic relationship between changes in pressure over the
height of a fluid column and gravity (acceleration
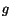 ), fluid density
), fluid density
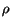 and the height
and the height 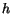 of the column:
of the column:
Equating these two gives a relationship between height of the
fluid above
the hole and the speed at which it spews forth,
The because the volume of fluid lost from the bucket must equal the flux of
fluid through the bucket's hole (with area 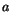 ),
),
and using the fact that (for a bucket with regular sides and constant cross
section in height) 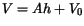 ,
,
Substituting in the relationship 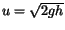 from above gives a
differential equation for height of the fluid,
from above gives a
differential equation for height of the fluid, 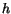 , as a function of time:
, as a function of time:
To solve equation (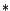 ) we use separation of variables. First, divide
both sides by
) we use separation of variables. First, divide
both sides by 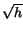 and multiply by
and multiply by 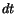 to separate
to separate 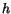 from
from 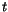 :
:
and now integrate both sides with respect to their variables. We will need
to use initial conditions as the bottom limits of integration, so let the
initial height at time zero be 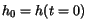 . Then:
. Then:
As a natural consequence of this solution one can calculate the predicted
time for the bucket to empty by setting 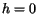 above, which gives
above, which gives
or

Testing the Torricelli model during the February 5 lab.
James Powell
2002-02-08




![\includegraphics[width=6.5in]{bucket.ps}](img2.gif)
![]() ) we use separation of variables. First, divide
both sides by
) we use separation of variables. First, divide
both sides by ![]() and multiply by
and multiply by ![]() to separate
to separate ![]() from
from ![]() :
: