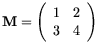 .
.
When you multiply a matrix by a scalar, that is by a single
number or parameter, multiplication is component by component:
When you add two matrices you do it component by component:
When you multiply a matrix by a vector, however, rows from the left are
multiplied by columns on the right:
When matrices are multiplied by matrices, the same rules are followed as with
vectors:
The Identity matrix (I) is the matrix that, when multiplied by either a matrix or
vector, doesn't change the result. That is, if M is a matrix and v is a vector, M![]() I = M and I
I = M and I![]() v =
v. In two dimensions,
v =
v. In two dimensions,
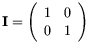 , and in three
dimensions,
, and in three
dimensions,
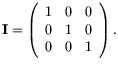
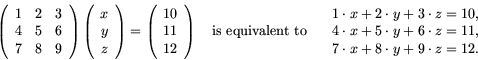
Think of ![]() as the coordinate of a point on a plane. If M
as the coordinate of a point on a plane. If M
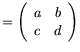 is a
matrix, then
is a
matrix, then
The easiest way to think of eigenvalues and eigenvectors is in
terms of the stretching and compressing of matrix maps. A matrix, M,
can only stretch/compress points in as many directions as there are - in two
dimensions there are only two directions, and in three dimensions there are
only three possible directions. An eigenvector, v is a direction in which
the matrix is a pure stretch, that is
M ![]() v =
v = ![]() v, where
v, where ![]() , the eigenvalue,
is the amount of stretching in that direction. Since we do not know, a
prioiri what the eigenvalue, eigenvector is, let v =
, the eigenvalue,
is the amount of stretching in that direction. Since we do not know, a
prioiri what the eigenvalue, eigenvector is, let v =
![]() . Then
. Then
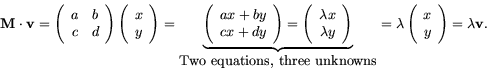
In higher dimensions eigenvalue/eigenvector pairs satisfy the matrix
equation