

Next: Numerical Solution using MATLAB
Up: Dribbling Big Gulps
Previous: Dribbling Big Gulps
In class we modelled the rate at which a Big Gulp empties through a hole of
area 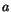 punched in its bottom. If
punched in its bottom. If 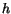 is the height of the fluid above the
hole, the pressure at the whole caused by the weight of the fluid bearing
down, is
is the height of the fluid above the
hole, the pressure at the whole caused by the weight of the fluid bearing
down, is
where 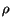 is the density of the fluid and
is the density of the fluid and 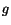 is the acceleration due to
gravty (so that
is the acceleration due to
gravty (so that 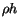 is the mass of fluid per area). Bernoulli's equation
gives that the (ideal) speed,
is the mass of fluid per area). Bernoulli's equation
gives that the (ideal) speed, 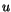 , to which a pressure differential
accelerates a fluid satisfies
, to which a pressure differential
accelerates a fluid satisfies
Consequently, the volumetric flow ratethrough a hole of area 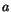 is
is
This gives a relationship between how volume changes and the height of the
fluid above the hole,
For regularly-shaped containers (like Big Gulps), the change in volume,
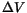 , over a small increment in time,
, over a small increment in time, 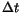 can be approximated as
can be approximated as
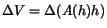 , where
, where 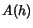 is the area of the fluid at the top
of the fluid (currently at height
is the area of the fluid at the top
of the fluid (currently at height 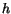 ). Thus,
). Thus,
We now arrive at a (relatively) simple differential equation for the height
of the fluid in the Big Gulp (neglecting ice):
The last part of the modelling for the Big Gulp is to determine how surface
area at the top of the fluid varies with the height of the fluid. As
indicated in the figure, the radius of a Gulp cross section varies linearly
with height according to
where 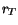 and
and 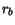 are the radius at the top (at least of the fluid in) and bottom of the Gulp
container and
are the radius at the top (at least of the fluid in) and bottom of the Gulp
container and 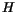 is the initial height of the fluid. Assuming that we have
not sat upon or otherwise deformed the container the cross sections are
circular, and thus
is the initial height of the fluid. Assuming that we have
not sat upon or otherwise deformed the container the cross sections are
circular, and thus
We need the derivative of 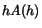 to proceed.
to proceed.
so
Thus,
Separating variables we arrive at
Integrating both side gives
And actually, this is about as far as we can go analytically. The next step
would normally be to solve for 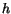 as a function of
as a function of 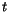 , but given the
expression for
, but given the
expression for 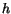 on the right hand side, we are out of luck. It is
possible to determine the free constant of integration,
on the right hand side, we are out of luck. It is
possible to determine the free constant of integration,
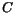 . Noting that at
. Noting that at 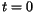
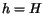 we can substitute these values into the
equation above and get
we can substitute these values into the
equation above and get
Fortunately, this is enough to predict the time at which the Big Gulp should
empty (at least according to the Torricelli model). Since the height of the
fluid will be 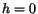 when
when
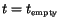 , the right hand side of
our integrated solution will be zero, giving
, the right hand side of
our integrated solution will be zero, giving
using 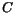 as given above.
as given above.
| |
| |
EXERCISE 6: Even though we can't find an analytic form for 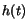 , we can plot it! Using , we can plot it! Using 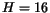 cm, cm, 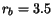 cm, cm, 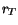 =10cm and a small hole diameter of
4mm, solve for =10cm and a small hole diameter of
4mm, solve for 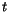 as a function of as a function of 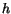 . Using MATLAB pick an evenly spaced
vector of . Using MATLAB pick an evenly spaced
vector of 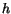 values between 0 and values between 0 and 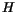 using linspace, and calculate the
corresponding values for using linspace, and calculate the
corresponding values for 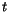 . Use plot(t,h) to plot these and verify
the emptying time expression above. . Use plot(t,h) to plot these and verify
the emptying time expression above. |
|
| |
|
|
| |


Next: Numerical Solution using MATLAB
Up: Dribbling Big Gulps
Previous: Dribbling Big Gulps
James Powell
2002-02-15
![]() punched in its bottom. If
punched in its bottom. If ![]() is the height of the fluid above the
hole, the pressure at the whole caused by the weight of the fluid bearing
down, is
is the height of the fluid above the
hole, the pressure at the whole caused by the weight of the fluid bearing
down, is
![]() , over a small increment in time,
, over a small increment in time, ![]() can be approximated as
can be approximated as
![]() , where
, where ![]() is the area of the fluid at the top
of the fluid (currently at height
is the area of the fluid at the top
of the fluid (currently at height ![]() ). Thus,
). Thus,
![\begin{displaymath}
\frac{dV}{dt} = \frac{d}{dt} \left[A(h) h \right] = \underbr...
...A(h) h \right]=- a \sqrt{2 g h}}_{\mbox{An ODE for
$h(t)$!}} .
\end{displaymath}](img77.gif)
![\begin{displaymath}
\frac{dh}{dt} = - a \sqrt{2 g } \frac{\sqrt{h}}{\pi \left[ r...
...
\frac{r_T-r_b}{H} h + 3
\frac{(r_T-r_b)^2}{H^2} h^2 \right]}.
\end{displaymath}](img84.gif)
![\begin{displaymath}
- a \sqrt{2 g } \ dt = \frac{\pi \left[ r_b^2 + 4 r_b \frac{...
...\frac12} +
3 \frac{(r_T-r_b)^2}{H^2} h^{\frac32} \right] \ dh.
\end{displaymath}](img85.gif)
![\begin{eqnarray*}
C- a \sqrt{2 g } t &= & \pi
\left[ r_b^2 \frac{h^{\frac12}}{\f...
...frac32} +
\frac65 \frac{(r_T-r_b)^2}{H^2} \ h^{\frac52} \right].
\end{eqnarray*}](img86.gif)
![\begin{eqnarray*}
C & = & \pi \left[ 2 r_b^2 \ H^{\frac12} +
\frac83 r_b \frac...
...rac{4}{3} r_b^2 +
\frac{2}{5} r_T \ r_b + 3 r_T^2 \right]. \\
\end{eqnarray*}](img89.gif)