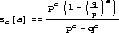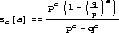Gambler's Ruin Web Page
Introduction:
This page contains an applet that will allow you to simulate the Gambler's Ruin
problem. The basic definition of the Gambler's Ruin problem is the following:
A person decides to try to increase the amount of money in his/her pocket by
participating in some gambling. Initially, the gambler in question has a certain
amount of money, say $a. The gambler decides that he/she will gamble until a
certain goal, $c, is achieved or there is no money left. If the gambler achieves
the goal of $c he/she will stop playing. If the gambler ends up with no money
he/she is ruined (thus the name of the problem). So, the gambler starts playing
a game of chance (e.g., poker, roulette, slot machines, etc.).
The question is:
What chance does the gambler have of achieving the goal?
In the version of the problem modeled in this page the following assumptions
will be made:
- The gambler chooses to play the same game over and over
- The gambler will bet the same amount, $1, each time.
- If the gambler wins they win $1.
- If the gambler gets to the goal amount, the gambler stops playing.
- If the gambler runs out of money, the gambler stops playing. There are
no lines of credit here.
Without these simplifying assumptions the problem is a bit too difficult. Due to
the fact that we are doing work on a computer, we also have to be aware of the
limitations. For example, a gambler could theoretically play forever by getting
into a repetitive sequence of winning and losing. Thus never achieving the goal
or running out of money. So, we will have to limit the number of times the
gambler plays in the simulations. You can assume that after that many times
playing the game the casino closes or throws the gambler out.
You can find a more thorough description of the Gambler's Ruin problem
here .
An Example:
Having an example in mind before starting up the simulations is a good idea.
A gambler with $10 decides to bet on black at a roulette table with the goal of
doubling the initial amount of money. This means the gambler will play until the
total amount of money he/she has is $20 or he/she has no money left.
NOTE: The probability of winning at roulette on a single play where the gambler
bets on black is 18/38.
The Gambler's Ruin Simulator:
The applet displayed below will simulate the simple Gambler's Ruin problem
defined above. To make the thing work you will need to understand how to input
values on the left side of the applet. The following is a list of inputs that
you will need to understand.
- Starting Amount: This is the amount of money that the gambler
starts with. In the example above this is $10.
- Goal: This is the amount of the money the gambler wants to leave
the casino with. In the example above this is $20.
- Chance of Winning a Game: This is the chance of winning a single
play of the game. The gambler will play the same game over and over. This
is the chance of winning each time. In the example above this is 18/38
which is about 0.4736.
- Number of Gamblers: In simulating the process we will need to be
able to simulate a number of gamblers. If this is set to 1 and the
simulation is done you will see a single gambler displayed in the text
area on the right. If there are more, the results from each gambler will
be listed.
- Maximum Number of Plays: In theory, a gambler could play forever
and never lose all the money or achieve the goal (e.g., win, lose, win,
lose, etc.). So, we need to put a maximum number of plays to be able to
guarantee that the gambler will not play forever. (Question: How will
this effect the results?)
So, for the example above, we can fill in the five text fields in the left
column below with
to try an example.
To run the simulator, just click on the Simulate button on the bottom.
The output from the simulation is explained below the applet.
The Simulator:
Output from Simulations:
There are several outputs you will see as you run the simulations. These are the
following:
- First, there are the two boxes showing how many gamblers achieved the
goal and how many gamblers were ruined. These are the first two boxes in
the two lines of output at the bottom of the text window.
- The next box in the first line is the approximate chance of achieving the
goal as produced by the simulations. The computation is to take the
number in the "Wins" box and divide this by the sum of the number in the
"Wins" box and the number in the "Losses" box.
- The first box on the second row of output boxes is the number of gamblers
who did not finish in the maximum number of plays allowed. This is an
important value in our work. (Why?)
- The last box on the second row is the value one would get from the exact
solution of the Gambler's Ruin problem (see the next section).
Exact Solution of the Gambler's Ruin Problem:
In this formula:
- a is the initial amount of cash.
- c is the goal the gambler is trying to achieve.
- p is the chance of winning
(0 < p > 1) on each
play of the game.
- q = 1 - p
Some Problems to Work:
Now that you see how the simulator works, you might want to try the following
problems that illustrate a few simple ideas. The idea behind the problems is to
get some idea of how the simulation compares to the exact result.
Problems:
- In this problem assume that a gambler walks into a casino with $5 and
wants to double that money. That is, leave with $10. Also, let's consider
the case when the gambler bets on black at the roulette table. Now, one
gambler at a time, observe the results of the gambler playing. That is,
run the simulator with one gambler. Tally the results on the
worksheet or a sheet of paper.
- Using the same paramters as the first problem, simulate the gambling
process using 32, 64, 128, 256, 512 1024 gamblers and tabulate the chance
of success. Discuss the relationship to the exact value as the number of
gamblers is increased.
- Using the same paramters as the first problem, simulate the gambling
process as the goal gets larger. That is, let the goal start at $10 and
gradually increase the goal. Discuss what happens.
- Using the same paramters as the first problem, simulate the gambling
process as the chance of winning a play of the game decreases. That is,
let the chance start at 0.4736 and gradually decrease the chance to about
0.2. Discuss what happens.
- In this problem simulate 250 gamblers using the values in the first
problem. Tabulate the results of the simulationn on the worksheet. Repeat
this process five times, tabulating the results. Next compare the results
to the exact answer for the problem. Finally, compute an average chance
of success using the five simulation results. Compare this to the exact
value and discuss all approximations obtained.
- Repeat the last problem with 500 gamblers.
- Discuss the differences in the results from the previous two problems.
Make a conjecture as to what would happen if the number of gamblers was
increased to 1000, 2000, and so on.
- In the simulations you will notice that some of the gamblers do not
finish the entire process. This means we do not know if the gambler would
be successful or not if allowed to continue gambling. What difference
will this make in any simulations we run? By increasing the number of
gamblers from a small number, say 10, to a larger number, say 1000, give
some justification for why these gamblers do not have a huge impact on
the overall simulation.