


Next: Project Goals
Up: Modelling Diseases - Discrete
Previous: Modelling Diseases - Discrete
Suppose 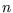 is the number of turns which have been played in the disease game,
and
is the number of turns which have been played in the disease game,
and 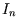 is the number of diseased individuals in the
is the number of diseased individuals in the 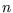 th turn of the
game. Then one may write
th turn of the
game. Then one may write
where 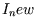 is the number of individuals which are newly infected during
turn
is the number of individuals which are newly infected during
turn 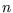 . A beginning model can be put together by assuming that the
distribution of infective hexes and individuals creating them is random. If
each infected individual `splats,' `sprays,' or `sneezes' into a zone covering
. A beginning model can be put together by assuming that the
distribution of infective hexes and individuals creating them is random. If
each infected individual `splats,' `sprays,' or `sneezes' into a zone covering
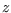 hexes, and the board contains
hexes, and the board contains 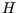 hexes, then an approximation for the
total number of hexes which are infectious at turn
hexes, then an approximation for the
total number of hexes which are infectious at turn 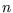 is
is
The number of individuals which are still susceptible to being infected on
turn 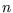 ,
, 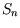 , is the total (
, is the total (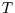 ) less the number of currently infected
individuals, that is
) less the number of currently infected
individuals, that is
Then the number of new infections can be approximated
Putting this all together gives an initial, discrete logistic model for the
propagation of disease:
In the case of the basic disease game, 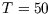 ,
, 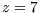 (six hexes surrounding
each diseased individual + the hex they stand in), and
(six hexes surrounding
each diseased individual + the hex they stand in), and 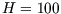 for the hex-grids
provided.
This model can serve as a foundation to build other, more advanced models
from.
for the hex-grids
provided.
This model can serve as a foundation to build other, more advanced models
from.



Next: Project Goals
Up: Modelling Diseases - Discrete
Previous: Modelling Diseases - Discrete
James Powell
2000-07-28
![]() is the number of turns which have been played in the disease game,
and
is the number of turns which have been played in the disease game,
and ![]() is the number of diseased individuals in the
is the number of diseased individuals in the ![]() th turn of the
game. Then one may write
th turn of the
game. Then one may write