Analytic Solution

As it turns out the logistic equation can be solved analytically, using separation of variables. First, separate the $P$ and $t$:

$$r \ dt = \frac{dP}{P \left( 1-P/K \right)}.$$

Our next goal would be to integrate both sides of this equation, but the form of the right hand side doesn't look elementary and will require a partial fractions expansion. That is, we wish to write

$$\frac1{P \left( 1-P/K \right)} = \frac{A}{P} + \frac{B}{\left( 1-P/K \right)},$$

where $A$ and $B$ are unknown constants. If we multiply on the left and right hand sides by $P \left( 1-P/K \right)$ (which is equivalent to putting the right hand side over a common denominator) we arrive at the equation

$$1 = A \ \left( 1-P/K \right) + B \ P = A + P \ (B - A/K).$$

Since there is no term with $P$ on the left hand side, we see that

$$B - A/K = 0 \quad \mbox{ or } \quad B=A/K.$$

If we set $B=A/K$ then we are left with $A=1$, and thus the partial fraction decomposition is

$$\frac1{P \left( 1-P/K \right)} = \frac{1}{P} + \frac{1/K}{\left( 1-P/K \right)}.$$

Now we turn to integrating the right hand side of

$$r \ dt = \frac{dP}{P \left( 1-P/K \right)} = \frac{dP}{P} + \frac{dP/K}{\left( 1-P/K \right)}.$$

First,

$$\int\frac{dP}{P} = \ln (P),$$

which is not too bad. For the second term, we must use a substitution $u=1-P/K$, which gives a differential $du = -1/K \ dP$. Thus we may write the second term on the right hand side as

$$\int \frac{dP/K}{\left( 1-P/K \right)} = \int \frac{-du}{u} = -\ln (u) = -\ln (1-P/K).$$

Putting all these terms together gives us

$$r t + c = \ln (P)-\ln (1-P/K) = \ln \left[\frac{P}{1-P/K} \right].$$

Here we have used the property of logarithms to equate the difference of the logs with the log of the quotient. The additional term, $c$, on the left hand side is the free constant of integration, which will be determined by considering initial conditions to the differential equation. Exponentiating both sides of the equation gives

$$C e^{rt} = \frac{P}{1-P/K},$$

which must be solved for $P$. However, it is convenient at this point to find out how the constant $C=e^c$ relates to the initial condition. Noting that at $t=0$ $P=P_0$ and substituting gives

$$C = C e^0 = \frac{P_0}{1-P_0/K} = \frac{P_0}{1-P_0/K} \frac{K}{K} =\frac{K P_0}{K-P_0}.$$

Solving now for $P$, we first cross-multiply to arrive at

$$\left(1-\frac{P}{K} \right) C e^{rt} = P,$$

and putting all terms including $P$ on one side of the equation,

$$C e^{rt} = P \left[1 + \frac{C e^{rt}}{K} \right] .$$

Solving now for $P$,

$$P = \frac{C e^{rt}}{1 + \frac{C e^{rt}}{K} } = \frac{\frac{KP_0}{K-P_0} e^{rt}}{1 + \frac{\frac{KP_0}{K-P_0} e^{rt}}{K} }.$$

Simplifying this expression by multiplying numerator and denominator by $(K-P_0) e^{-rt}$ gives

$$P = \frac{K P_0}{P_0 +(K-P_0) e^{-rt}}.$$

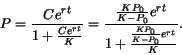
	EXERCISE 2: Compare this exact solution with the Euler-type numerical solution you computed above. How does the accuracy change as $N$ is decreased?

	EXERCISE 3: In class we discussed how direct conversion of resources to offspring and a finite resource base results in the logistic equation. Suppose now we want to investigate the effect of per-capita `harvesting' of the population, that is, to see what happens when we subtract a given fraction, $h$, of the population per time. This changes the logistic equation to $$\frac{dP}{dt} = r P \left(1 - \frac{P}{K}\right) - h P, \quad P(t=0) = P_0.$$ Solve this new equation using the separation of variables technique. What is the effective carrying capacity in this situation?